4.1. Introduction

Although mathematics and music have been linked since the time of the ancient Greeks (Benson 2006), the link between music and statistics has been relatively recent, thanks to the progress in computer technology and the avaibility of digitized scores (musical notation). Unlike Western classical music where the scores are fixed, Indian classical music is quite extempore. This means we can only analyze such a performance provided it is recorded first (so that the score can be fixed). In spite of the power which statistical methods bring to modeling, it is still quite a challenge to statistically model a performance of Indian classical music given that, despite the binding rules of the raga (fixation of notes, typical note combinations and how they are to be used in a raga etc.) the artist still has infinite freedom to express himself. The present paper gives a statistical analysis of a vocal rendition of the raga Ahir Bhairav rendered by a trained vocalist and D. Mus. from Banaras Hindu University, India.[1] Before going into the analysis, we take a look at some of the basic features of Indian Classical music in general and raga Ahir Bhairav in particular.

A raga, the nucleus of Indian classical music, is a melodic structure with fixed notes and a set of rules characterizing a certain mood endorsed through performance (Chakraborty et al. 2008a). Here, the melodic structure refers to sequences of notes often with micro-pitch (sruti) alterations and articulated with an expressive sense of timing. Longer phrases are built by joining these melodic atoms together leading to a tonal hierarchy (Chordia & Rae 2007). For more on tonal hierarchy in North Indian music, we refer the reader to Castellano et al. (1984).

The notes in the raga are called swars. The seven swars Sa, Re, Ga, Ma, Pa, Dha and Ni in Indian music correspond to Do, Re, Mi, Fa, Sol, La and Si respectively in Western music. The stay notes permissible in a raga are called nyas swars. The terms Vadi, Samvadi, Anuvadi, Alpvadi and Vivadi swars refer to, respectively, the most important, the second most important, the important but not vadi or samvadi, the unimportant or weak, and the non-permissible notes respectively. Ragas can be grouped according to thaats depending on the manner in which permissible notes are fixed. This is similar to the notion of mode in Western music. There are ten thaats in North Indian classical music and many more in the South. The ten thaats are Bilawal, Kafi, Khamaj, Purvi, Bhairav, Kalyan, Todi, Marwa, Bahairavi and Asavari. For Example, {Sa, Sudh Re, Komal Ga, Sudh Ma, Pa, Sudh Dha and Komal Ni} represents the Kafi thaat and accordingly, ragas Bageshree and Bhimpalashree both belong to this thaat as they use these notes. Not all ragas can be easily placed in a thaat, however. E.g. our own example, Ahir Bhairav itself creates a confusion! Ragas are also classified according to jati depending on the number of notes allowed in ascent (arohan) and descent (awarohan). The terms Aurabh, Sarabh and Sampoorna refers to five, six and seven notes being used respectively. For example, Ahir Bhairav in our case is a Sampoorna-Sampoorna raga as it allows seven notes in ascent and seven in descent (detailed later). The pakad (catch) is a defining phrase or a characteristic pattern for a raga describing its movement. For example, {Pa Ma Ga Ma Ga} is a tell-tale sign of raga Bihag.[2]

In Western music, a piece of music is in a certain key, i.e., it uses the notes of a particular major or minor scale. The harmonies and counterpoint[3] developed using those notes are crucial. In contrast, Indian classical music does not emphasize harmony and does not feature counterpoint. The interest and complexities lie in melodies and rhythms. A typical Indian classical music performance features a single melody instrument or voice (in case of voice, it is shadowed by one or more accompanying melody instrument like a harmonium, a sarangi or a violin) accompanied by percussion such as a tabla and a drone (generally Sa-Pa or Sa-Ma, in exceptional cases Sa-Ga or Sa-Dha) providing a harmonical base (well, this is perhaps the only place we have a harmony!) rendered by tanpura. The artist generally “stars” with an alaap in which the raga is elaborated without percussion and then plays a song-like composition called “gat” where the percussion begins. The drone is present throughout the performance. (For more on Indian Classical music, see Menon (2007) and Priyamvada (2007). Readers familiar with Western music but new to Indian music will benefit from Jones (2009)).

4.2. Analysis of the Raga Ahir Bhairav

Raga: Ahir Bhairav []

Musical features:

• Thaat: Not specific, generally taken as “Mishra Bhairav”
• Arohan (ascent): S r G M P D n S
• Awarohan (descent): S n D P M G r S
• Jati: Sampooorna-Sampoorna (7 notes allowed in ascent and 7 in descent)
• Vadi Swar (most important note): M
• Samvadi Swar (secondmost important note): S
• Prakriti (nature): Restful
• Pakad (catch): S, r G M, G M r, n D, n r S
• Nyas Swar (Stay notes): M and S
• Time of rendition: morning (pre-dawn)

Abbreviations:
The letters S, R, G, M, P, D and N stand for Sa (always Sudh), Sudh Re, Sudh Ga, Sudh Ma, Pa(always Sudh), Sudh Dha and Sudh Ni respectively. The letters r, g, m, d, n represent Komal Re, Komal Ga, Tibra Ma, Komal Dha and Komal Ni respectively. A note in normal typeface indicates that it belongs to middle octave; if in italics, it is implied that the note belongs to the octave just lower than the middle octave, while bold typeface indicates that it belongs to the octave just higher than the middle octave.

The present analysis is based on a vocal performance (Sa set to natural C) and recorded by a laptop at 44.100 KHz, 16 bit mono, 86 kb/sec mode. Solo Explorer 1.0 software, a wave-to-midi converter and an automatic music trascriber for solo performances (hence the name), was used to generate the onsets and the fundamental frequencies of the notes. The software generates the notes in Western notation, but we generated the same in Indian notation, crosschecking with MATLAB; the technical details may be found in (Chakraborty et al. 2008a).

4.2.1. Statistical Analysis

What is the importance of modeling from a musical perspective? It is only through modeling that we can answer questions such as “what is the probability for the next note to be a vadi or a samvadi swar?” By a vadi swar is meant that note which plays the most significant role in expressing the raga. A samvadi swar similarly is the second most significant note. When we say that a vadi swar is so called as it plays the most significant role in expressing the raga, what it tells us, apart from elaborating the mood characterizing the raga, is whether the raga is purvanga pradhan (first half more important) or uttaranga pradhan (second half more important), depending on whether the note in question is one of the notes from Sa to Pa or from Ma to Sa. As Ma and Pa fall in both the halves thus created, expert guidance is needed to decide the more important half in case the vadi swar turns out to be one of these two notes. Also the vadi swar gives us a rough idea of the ideal timing of the raga’s rendition. For a purvanga pradhan raga, such as Pilu, the timing broadly is 12 a.m.. to 12 p.m. For an uttaranga pradhan raga, such as Bhairav, the time period is somewhere between 12 p.m. and 12 a.m. (Chakraborty et al. 2008a).

In the book Music and Probability (Temperley 2007), David Temperley has investigated music perception and cognition from a probabilistic point of view by means of extensive usage of Bayesian techniques.

When an artist is rendering a raga, it is not possible to say definitely which note will come next. One can, still, assign a probability for a particular note to come. Now, let us direct our attention to a particular note say Sa (or Do), the tonic. One question of interest is: at every instance, does Sa have the same probability of occurring? The same question can be raised for every other note permissible in the raga. If this probability is fixed, our model is multinomial, otherwise quasi-multinomial (see also the appendix). Additionally, independence of notes overall is also required, but this is weaker than mutual independence and hence, as we shall see, generally fulfilled. If the performer is a novice and can use a wrong note (vivadi or varjit swar) by mistake, such a possibility, W (for wrong), should also be kept in mind to make the list of possible notes exhaustive. One then asks for W’s probability as well! This is not required here as we are analyzing an accomplished vocalist. Since a note can be vadi, samvadi, anuvadi, alpvadi or vivadi with respect to a raga, it is logical that its probability is raga-dependent. For example, Pa, being alpvadi in Bageshree, will have a small probability there, but in Kafi the same note has a high probability (one musical school holds Pa as vadi in Kafi; another school holds Komal Ga as vadi; even if Pa is not a vadi, it definitely is anuvadi). Again, Pa is vivadi for Malkauns, and hence its probability there is zero.

We first make a comparative study of relative frequencies (ratio of number of occurrences of the note to the total number of detected notes in the specified time period) of individual notes as observed in the first 30 seconds, the middle 30 seconds and the last 30 seconds with the same for the whole minute performance. Tables 1.1-1.4 summarize the results. In the present performance of one minute’s duration, 78 notes were detected using the text file of fundamental frequencies generated by Solo Explorer against time and the database of the same for notes, using Chebushev’s inequality with 6-sigma limits; (see Chakraborty et al. (2008a) for more details).

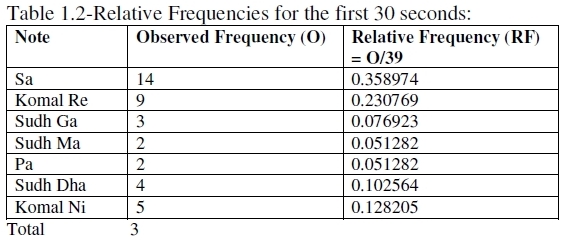
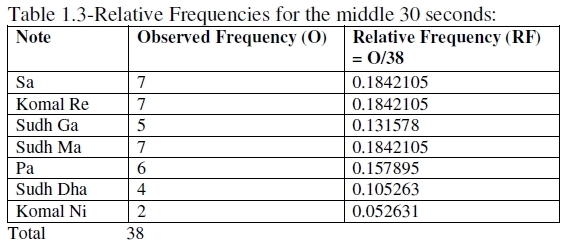
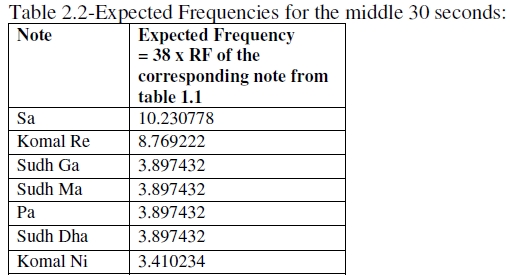
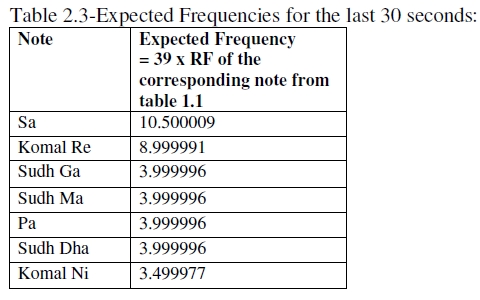
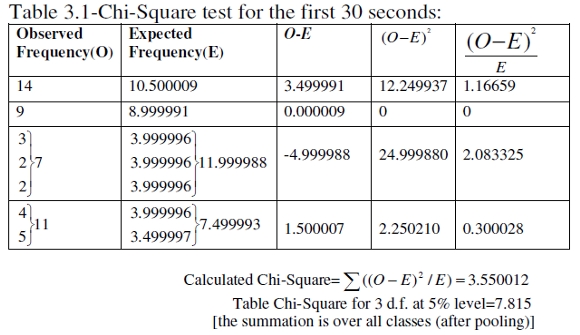
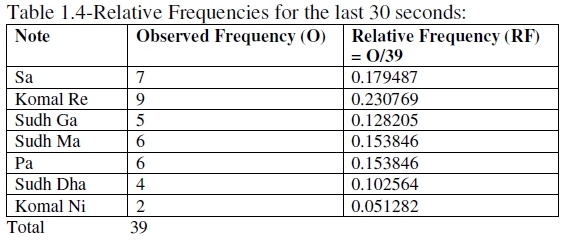We test for the possibility of a multinomial fit (see Gupta & Kapoor (1983) and appendix). Now, we have the formula: Expected frequency of a note in a time period = Total notes detected in the time period x Relative frequency of the note for the whole performance, because relative frequency of the note for the whole performance may be taken as a probability of arrival of the note. For example, in the first 30 sec, we had 39 notes. The probability of Sa is 0.269231 (table 1.1). Hence the expected number of Sa in the first 30 sec = 39 x 0.269231 = 10.500009. We thus prepare tables 2.1-2.3.

Next we perform Chi-Square goodness of fit tests (tables 3.1-3.3). These tests are non parametric (meaning “distribution free”) (Gupta & Kappor 1983).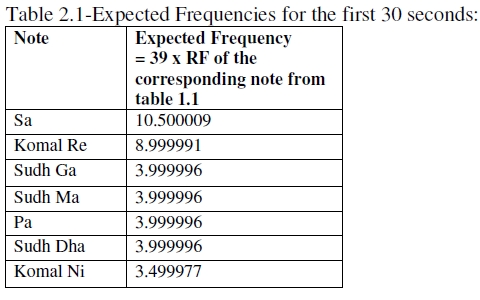

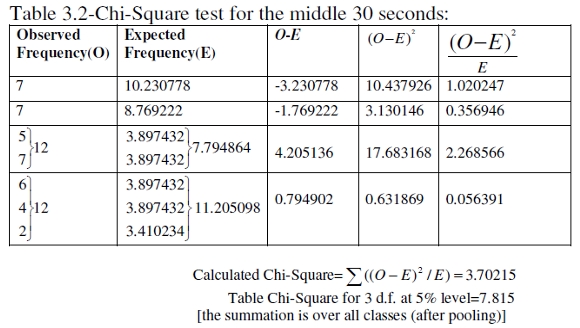
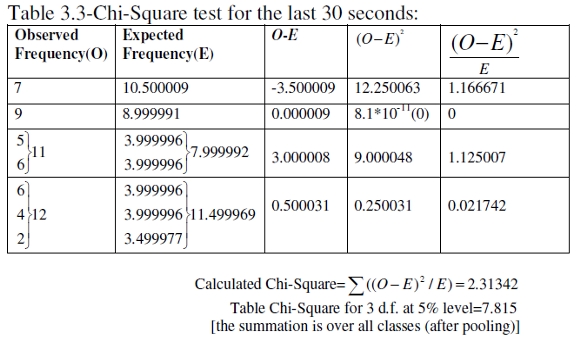Interpretation:
Since all calculated Chi Square values are less than corresponding table Chi-square values at the 5% level, the three fits are good at this level for table 2.1-2.3, whence we can say that the overall relative frequencies of the notes for one-minute performance are being maintained in three individual time periods of 30 seconds each. In other words, the probability of arrival of a note is not varying considerably, a prerequisite for multinomial distribution. The other requirement, namely, overall independence of the notes was verified using a run test of randomness (see Gupta & Kapoor (1983) and appendix). This was accomplished by verifying the sequence of the digits 1, 2…7 coming in a random order as per performance where the digit 1 represents Sa, 2 stands for Komal Re etc.. Smallest value of calculated Chi-Square is obtained for the last 30 seconds. This is the best representative of the whole performance. We, caution the reader, however, that the goodness of fit is an overall fit considering all notes together. If we go for individual notes, especially the Vadi Swar Sudh Ma and the Samvadi Swar Sa, we do notice unwanted fluctuations. Since important notes are those in which the probability of arrival stabilize in a short period of time, apart from appreciable high relative frequency (Chakraborty et al. 2008a), the contradiction suggests that although a multinomial fit can be taken as a working model at a 5% level of significance, a quasi multinomial fit would certainly be a better option.

4.2.2. Analysis of Transitory and Non-Transitory Pitch Movements Between the Notes

According to Strawn (1985), a transition includes the ending part of the decay or release of one note, the beginning and possibly all of the attack of the next note and whatever connects the two notes. Hence, in addition to the study on modeling a performance, a count for distinct transitory and similar-looking non-transitory frequency movements (but which possibly embed distinct emotions!) between the notes was also also taken. In the characterization of ragas in Indian music, not only the notes and note sequences but also how they are rendered are important. There is a concept known as alankar in Indian music meaning ‘ornament’ (of course in a musical sense). The shastras have categorized alankars into Varnalankar and Shabdalankar (ITC Sangeet Research Academy 2009). The varnas include sthayi (stay on a note), arohi (ascent or upward movement), awarohi (descent or downward movement) and sanchari (mixture of upward and downward movement). This classification of alankars relates not only to the structural aspect of the raga, but also the raga performance. A non-transitory movement would depict staying on a note for short or long duration. In the graph it resembles a horizontal line with some tremor (the tremor is because pitch is never steady).

In the present Ahir Bhairav performance, we found the following:

Among the 12 rising transitions, interestingly, four each were convex, concave and linear. But for the 12 falling transitions, as many as eight were concave, only one convex and the remaining three linear.

Interpretation:
The rising and falling transitions are equal for Ahir Bhairav. This means it is difficult to classify raga Ahir Bhairav as one of Arohi or Awarohi varna, i.e. the tendencies to ascend and descend are equal. The substantial number of non-transitory movements and fewer mixed transitions indicate frequent staying on the notes which is only expected in a morning raga as morning is peaceful. See also the inter-onset interval graph in fig.1.2. Since linear transitions are fewer in number compared to nonlinear transitions both for rising and falling cases, it suggests possible use of meend, i.e. a continuous transition, in the form of a glide, from one note to another. The exact musical interpretation of concave and convex rising and falling transitions is under investigation, and further study requires a fairly large database for which we are consulting with ITC Sangeet Research Academy, Kolkata. Lest the reader should wonder why there are 50 transitory and non-transitory movements while we had 78 notes, it suffices to point out that notes were detected from the text file using the database of note fundamental frequencies and Chebyshev’s inequality (see Chakraborty et al. 2008a) and not graphically, whereas transitory and non-transitory movements could be observed only from the graph. Although Solo Explorer graphs also generated the notes in Western notation (each note corresponds to a vertical line; there were 51 vertical lines in the graph) we could generate more notes (78) from the text file adopting our technique. This is in fact, as stated in Chakraborty et al. (2008a), one of the strengths of the statistical approach. The software can miss a note graphically if the amplitude is low. We can still catch it from the text file depicting a succession of nearby fundamental frequencies matching with those of notes in our database (Chakraborty et al 2008a). This database was formed by playing each of the twelve notes in three octaves, noting the means and standard deviations of their fundamental frequencies and applying 6-sigma limits of the powerful Chebyshev’s inequality which is distribution free (Gupta & Kapoor).

Fig.1.1 gives a sample of Solo explorer graph of Ahir Bhairav.

Fig 1.2 gives an inter-onset-interval graph for metrical analysis.

Interpretation:
Notes are said to be in rhythm if the inter-onset interval times (time difference between two successive onsets) are equal. The x-axis in the graph gives the serial number of note pair (successive) while the y-axis gives the corresponding inter-onset interval time in seconds. It is clear from the graph that there is not much rhythm as the heights of the peaks are varying considerably. This is expected as the artist rendered only alaap (introductory description of the raga without percussion; here the artist elaborates the mood of the raga without rendering any bandish - a song-like structure). The first author adds thatgenerally, metrical analysis is omitted by music analysts if only alaap is rendered. However, from my personal experience of playing North Indian classical music on the flute during my younger days and the harmonium presently, I can assure you that I almost always happened to play short sequences which were in rhythm that were part of a long musical sentence, even during the alaap portion of a raga rendition. Therefore a meter should always be fitted to be on the safe side. This is, however a purely subjective piece of opinion. A second point to note is that several peaks are rising to appreciable heights, indicating more staying on the notes. This is what is expected in a morning raga such as Ahir Bhairav given that morning is expected to be peaceful. It may be of interest to compare such findings with those in an evening raga such as Yaman (Chakraborty et al 2008d) or a night raga such as Malkauns for example.

Remark: We are omitting melodic study of notes. One reason is that multinomial modeling as used in the paper is a count-based modeling, as opposed to the conventional melody-based modeling practiced by other researchers such as Temperley, Eerola and Pearce to name a few, and hence can be accomplished easily without having to do melodic analysis. Another reason is that purity of the raga and melodic properties of the notes are two different things. It is possible to include some additional notes in the raga (in which case it is mishra Ahir Bhairav), make it more colourful, destroy the sudh nature or purity and yet increase the melodic properties of notes! The artist,[4] who rendered the Ahir Bhairav performance refrained from such practices.

Nevertheless, studies of melodic properties of notes are useful as they tell whether notes are part of motifs (configurations) that are similar to many other motifs that occur elsewhere in the score.part. See Chakraborty et al. (2008b) where two ragas (Kafi and Sindhu) which use the same notes were statistically compared with respect to metric, melodic properties of notes and other characteristics.

4.3. Conclusion

While it is true, as pointed out by one of the referees, that “. . . statistics are a means for description that does not ‘explain’ the findings at hand. In regard of the analysis of a rendition of a certain rag (Ahir Bhairav), the statistical analysis can not directly model the decision processes of the artist who performs this rag. . .”, the following facts remain: (i) one can still raise a Bayesian question like “given a note sequence, what could be the musical structure in the performer’s mind?” which is precisely one of the issues addressed by Temperley (2007), (ii) from the point of view of the analyst or the critic, there is no unique way of analyzing a performance, whence a realistic theory of a musical performance cannot be purely causal or deterministic (Beran and Mazzola 1999). In addition, (iii) musicians are themselves confused about Vadi-Samvadi selection in certain ragas such as Rageshree (see how statistics has been used to resolve this issue in Chakaraborty et al. 2008c), Bageshree, Hamir, Shankara, etc. Although this confusion did not exist in the case of Ahir Bhairav, still other questions such as “what is the probability that the next note is a Vadi swar” could be answered only through statistical modeling. The conclusion is that statistics and probability are likely to play important roles in analyzing a musical performance.

4.4. Appendix

Multinomial distribution
Consider that n independent trials are being performed. In each trial the result can be any one of k mutually exclusive and exhaustive outcomes e1, e2…ek, with respective probabilities p1, p2…pk. These probabilities are assumed fixed from trial to trial. Under this set up, the probability that out of n trials performed, e1 occurs x1 times, e2 occurs x2 times ….ek occurs xk times is given by the well known multinomial law (Gupta and Kapoor 1983) {n!/(x1! x2!...xk!)}p1x1p2x2…pkxk where each xi is a whole number in the range 0 to n subject to the obvious restriction on the xi’s, namely, x1+x2+…..+xk=n. For this distribution, E(xi)=n(pi) and Var(xi)=n(pi)(1-pi), i=1, 2…….k. Cov (xi, xj) = -n(pi)(pj).

One can then calculate the correlation coefficient between xi and xj as
Cov(xi, xj)/√[Var(xi)*Var(xj)].

If the probabilities vary we shall get a quasi multinomial distribution.

Run Test of Randomness
Let x1, x2…xn be n observations arranged in the order of arrival or occurrence. Calculate their median. Now examine each observation and write L if it is less than the median and M if it is more. If equal, write either L or M. You will get a sequence such as LLMLLLMMMMLLMMMMM…etc. Count the number of runs = U. A run is a sequence of letters of one type preceded and/or followed by letters of another type. For example, LLMLLLMMMM has four runs (counting one each for LL, M, LLL, MMMM). Under the null hypothesis that observations are random, U is a random variable with E(U)=(n+2)/2 and Var(U)=(n/4)[(n-2)/(n-1)]. For large n, the statistic Z = [U-E(U)][+√Var(U)] follows standard normal distribution. If the absolute value of Z >= 1.96, the null hypothesis, that the observations are random, will be rejected at 5% level of significance, otherwise it may be accepted.