| The Colorado Cookbook | Bb | Cm7 F7 | Bb | Cm7 F7 | Bb7 | Eb7 E°7 | Bb | Cm7 F7 |
| Jazz Fake Book | Bb | ./. | ./. | ./. | ./. | ./. | ./. | ./. |
| The New Real Book | Bb6 Gm7 | Cm7 F7 | Bb6 G7 | Cm7 F7 | Bb6 Bb7 | Eb6 Ebm6 | Dm7 Gm7 | Cm7 F7 |
| The Real Book | Bb∆ G7 | Cm7 F7 | Bb∆ G7 | Cm7 F7 | Fm7 Bb7 | Eb∆ Ebm6 | Bb∆ G7 | Cm7 F7 |
|
JMM 4, Winter 2007, section 4 4.1. Improvised Signs Musical semiotics is often approached through application of the Peircean sign system. In the present study I shall use an alternative approach, based on Saussurean semiology as developed by Hjelmslev (1961), Greimas & Courtés (1979) and Brandt (1990). According to this tradition the sign-function is basically seen as a cognitive phenomenon which is evoked in response to perceived elements. The tenor of my presentation will be the view that human beings, including jazz musicians, by nature are actively engaged in making sense of their lives and the world they live in, and that such a semiotic behaviour can be studied cognitively and neurobiologically inside a semiological paradigm. Using a famous bebop solo as a paradigm example, I shall consider the dynamic relationship between the sign function, its content (the signified) and its expression (the signifier) (see example 4 below). Developing the content structure we shall then investigate its diachronic aspect on the assumption that the metric/harmonic foundation of the chorus represents a simple story, a proto-narrative, which is being told repeatedly by different voices, under different circumstances, emphasizing different points and articulating varying spectres of mood, tempo and intensity. The notion of the “embodied sign function”, which follows from considering the sign to be a cognitive phenomenon, leads to two important conclusions.[1] First, the musical phrase evokes a cross-modal response, which can be interpreted as the mental representation of a physical gesture;[2] and second, as I shall propose in this paper, the idea of musical form - in this case the chorus of a jazz improvisation - is represented in the mind/brain as structured movement through space. 4.2. The Flexible Changes The advent of bebop in the 1940s marked a significant change of the improvisational strategy in jazz (see for instance Deveaux 1997, Gillespie 1979). In early jazz and swing the improvisation unfolded from the melodic form, but in bebop – and beyond – improvisation found its foundation in the harmonic structure of the piece: “the changes”. In order to express oneself fluently within the new jazz idiom, one had to become an adept in music theory and develop the ability to design harmonic structures that would promote the type of improvisation one was looking for. The reharmonisation of well known tunes was introduced as part of the working-schedule for a jazz musician, and, as a long-range result of this, the most widely shared tunes today exist in a broad variety of manifestations, in which the harmonisations differ to a larger or smaller degree reflecting the personal style of the designer. This development has led to the existence of a profusion of Fake Books, where many songs appear in different harmonisations, depending not only on which recording has been transcribed, but also on the musical philosophy of the transcriber. Consider the following four harmonisations of the A-section of Sonny Rollins’ classic Oleo, which harmonically is a simple I Got Rhythm-structure (see Example 1). The differences presented here reflect varying approaches to improvisation on an 8-bar A-section of a Rhythm-structure in Bb, ranging from the simplistic prescription in Jazz Fake Book to the detailed two-chords-to-a-bar notation of The Real Book and The New Real Book.
Example 1
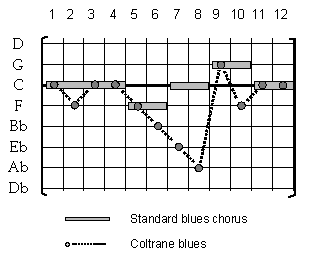
We see that different notations can point to the same underlying structure, which in three of the four examples presented includes a move to the subdominant level in bars 5 and 6. Here we are dealing with a dynamic phenomenon. In Chomskyan terms we could speak of a surface structure, represented by the written chords, and a deep structure, the implied instruction to “vamp” in Bb.[3] This raises a number of questions concerning the dynamic interrelationships between the different structures involved, not least the remarkable fact that most musicians, without further thought, would identify an AABA-structure built from any of the tokens met in Example 1 as the type: “Rhythm-changes”. So we see that Rhythm-changes could be many things, and could be interpreted in many different ways. 4.2.1. Blues and the Abstract Truth Let us look at another example: the blues. The blues form can be varied almost indefinitely and still be a blues. Even across genres like rock and jazz the form will be consistent and self-explanatory: 3 x 4 bars, where you move to the subdominant in bar 5-6 and touch upon the dominant in bar 9-10. Tied to the idea of the blues is a specific flavour of phrasing and a surprising tonal flexibility: even on top of a sophisticated schema of many changes (like the Parker-example below) it is still possible to play the same few notes derived from a simple blues scale, as for instance (in C) C-Eb-F-G-Bb, and it will sound great as long as you can maintain the anticipation of an eventual return to the basic tonality.
Example 2 Listen: Hendrix [
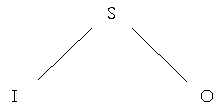
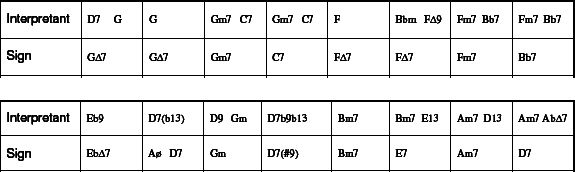
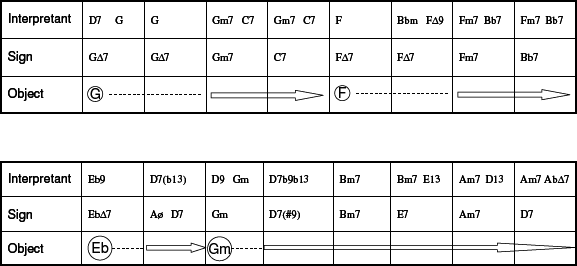
Example 2 presents four different interpretations of the blues structure[4] (in order to facilitate comparison they have been transposed to the key of C). They appear to be very different, but they are all in fact interpretations of the same basic structure. This prototypical blues structure is presented graphically in example 3, where it is represented by horizontal boxes outlining a path through a two-dimensional musical space, where time runs horizontally from left to right, while the tonal dimension runs vertically as a continuum of the cycle of 5ths with the tonic - in this case C - in the “zero” position. A graphic representation like this is an example of what I would call metaphorical visualisation of musical material, which is quite common. It is based on what cognitive science calls “mappings” between properties in different domains, and facilitates the understanding of complex information, much the same way that metaphors in language do (for a thorough discussion of this phenomenon see Zbikowski 2002). In this case, the vertical presentation of bars as numbers on a line is derived from a mapping between TIME and MOVEMENT (compare the metaphor TIMELINE). The vertical presentation of tones is similar to the metaphoric idea of scales, where the tones are pictured as steps on a ladder (compare with the Italian word ‘scala’ which means staircase), and the mapping is derived from the SCALE schema and based on the idea that HIGH-IS-UP and LOW-IS-DOWN (se Johnson, 1987). The embedding of the musical experience in a quasi-physical space is tied to the whole idea of embodiment of musical meaning, which I have dealt with elsewhere(Kühl, 2002; Kühl, in print; Kühl, under prep.). In example 3 we can compare the path of the basic blues structure to the path marked by the Coltrane-blues. Although the two paths clearly differ, their claim to similarity is based on the fact that they coincide at three salient points in the virtual space represented:[5] bars number 1, 5 and 9, indicating that metrical considerations are powerful in musical thinking. We can compare the variations of the blues with a game, in which you move along a given route, but the rules only command you to touch on 3 specific places at 3 specific points of time: the rest of the time you can take a deviating route if you wish to do so. Musical form can thus be conceived as a mental map in the mind/brain (Hutchins 1995), which metaphorically and cross-modally outlines a path through a virtual space. Stylistic conventions and personal preferences provides the map with a set of rules for specific actions at specific times, at the same time leaving the subject, who is travelling along the path, free to deviate from the shortest way between points, and to choose his own manner of locomotion limited only by conventions and preferences. This is a rich approach to musical analysis, opening many new ways of explaining differences in genre, style, culture etc., but for the present we shall limit ourselves to the discussion of jazz improvisation. The kind of map employed here I shall call a Metric/Harmonic frame (M/H frame) for improvisation, and it will be dealt with in more detail below. 4.2.2. Reharmonisation In chord based jazz improvisation the flexibility of the musical form is tied to the disciplines of chord substitution and reharmonisation. Before we proceed, I wish to introduce some of the methods that jazz musicians have developed for the reharmonisation of given chord structures, as I intend to apply these rules as analytical instruments in the context I have developed. Extant analytical methods are limited in their approach, as they only concern themselves with the receptive or perceptive side of musical meaning production, leaving out the productive side. I wish to argue that if our set of analytical tools is to be considered adequate, we must take into account how music was conceived of in the first place, and here jazz improvisation, as being performed on-the-spot, provides us with a more suitable template than music which was written down a long time before its performance. Looking again at example 3 we see that instead of the usual path through two bars in F followed by two bars in C and on to G, Coltrane proceeds along an alternative path, which involves four positions on the cycle of fifths in the subdominant direction: F7 to Bb7 to Eb7 to Ab7, where the penultimate chord, the Ab7, is only one half step from the target, the G7 in bar 9. The Ab7 can then be reinterpreted as a tritone substitution for the dominant of G7, and with this elegant move we arrive at the target on time. This is one example of reharmonisation used creatively. Another example is the Mingus-blues, where the F7 in bars 5-6 is substituted with an Fm7 (a common enough switch called modal interchange – see Nettles & Graf 1997), which is subsequently substituted with the Ebm7-Ab7 construction. Likewise in bars 9 through 11 Mingus substitutes the G7 to F7 to C7 of the basic blues structure with a sequential device similar to the one Coltrane employed. Starting on Am7-D7 in bar 9 (substituting the G7 with its IIm7-V7) it follows the sequential logic through Gm7-C7 in bar 10 (touching the G root reinforces familiarity, but is not essential for the device to work), and on to Fm7-Bb7 in bar 11. This delays the arrival of the tonic chord, and substitutes the expected tonic in bar 10 with another common substitution: IVm7-bVII7 instead of IIm7-V7. Jazz improvisation is full of devices like these, and furthermore, they tend to work in both directions. For instance a simple rule for substitution says that when we meet with two bars of a V7 chord, we are free to substitute the chord in the first of these bars with a IIm7: V7-V7 can become IIm7-V7 (the metrics can even be varied, just as long as you end up on the V7). Similarly we could say that the chord sequence IIm7-V7 could be read as V7-V7. Another substitution rule allows you to introduce a dominant chord, when a tonic chord takes up ample space: I∆7-I∆7 becomes I∆7-V7. This could similarly be reversed this so that the construction I∆7-V7 could be simplified and seen as I∆7-I∆7 (and here, too, the metrics are variable). The examples used here are drawn from the literature. We should bear in mind, however, that rules for reharmonisation demonstrate the flexibility of a set of changes for the performing jazz musician: substitutions are performed on-the-fly, without prior arrangement. We shall study this phenomenon more closely, using a specific Charlie Parker solo as an example. In what follows the improvisational act will be seen as a process of signification, in which the given changes (the Harmonic Text) constitute the sign function, which mediates between the signifier (Parker’s improvised reharmonisations and chord substitutions) and the signified (the Metric/Harmonic Frame).
Example 4 The Saussurean sign function
 4.3.1. The Musical Sign Function: The Harmonic Text Some of the oldest surviving examples of bebop were recorded at a session in Los Angeles in 1946, with a Charlie Parker-led group including a very young Miles Davis on trumpet. The session produced a number of classical Charlie Parker solos, including the famous alto-break in A Night in Tunesia and the piece we will discuss here, Ornithology (see example 5). We shall approach the discussion from the level of the Harmonic Text. The musicians involved in the session were all well acquainted with the changes for Ornithology, as it is based on the standard How High the Moon. Therefore it is extremely unlikely that they would be playing from lead sheets or written chords: they would simply know the song. Nevertheless, as discussed earlier, knowing the song does not mean sharing the same concept of the harmonisation of the song. Just as was the case with the Rhythm-structure, several possible interpretations exist; in fact most fake books today provide deviating harmonisations of Ornithology. In order to be able to play well together, the musicians must have had one particular harmonisation in mind, with the possibility of minor deviations at strategic points. This mental picture would be a reharmonisation of How High the Moon, involving a number of applications of one of bebop’s most important devices: the II-V-I progression. Such a shared notion of a set of changes to use for improvisation I shall call the Harmonic Text (HT),[6] the text that is to be collectively interpreted (see Berliner, 1994). I have reconstructed the changes of Ornithology in example 5 above. 4.3.2. The Specific Version In the solos, the HT is being interpreted in a personal way. Leaving aside for the present investigation the melodic gesturing of the improvisation and other musical parameters (for a study of the melodic gestures in Ornithology see Kühl, in print), we shall concentrate on some of the harmonic deviations from the text. The first 16 bars of Parker’s solo are shown in example 6 below. Parker does not follow the HT slavishly, but performs an online reharmonisation following a number of substitution rules. The harmonic variations, analyzed from the sheet music, are shown schematically in example 7 below.
Example 7
 In the first bar we encounter one of the rules we met earlier, that when we have a I chord we can substitute it with the progression V7-I. In bars 3-4 we meet the other rule discussed earlier, which says that a V7 can be substituted with a IIm7-V7 and vice versa; or in other words that the metrics of the IIm7-V7 progression can be treated quite freely. The Bbm in bar 6, which serves as a passing chord, is another common substitution of F with the IVm of F. And in bars 7-8 we meet the free rhythmical treatment of the IIm7-V7 progression. In bar 9 the Eb∆7 is substituted with an Eb7, a substitution called modal interchange, where chords with the same root but with different primary scales are considered to be interchangeable.[7] The principle of modal interchange again applies to the substitution of D7 with D7(b13) in bar 10, while at the same time IIø is omitted according to a now well known principle. Bars 11 through 16 provide more examples of the two rules of the interchangeability of I, IIm7 and V7. In bar 16 the Ab∆7 provides stability for a melodic chromaticism, while at the same time combining a tritone substitution (Ab7 for D7) with a modal interchange (Ab∆7 for Ab7). So we can see that all the “changes of the changes” that Parker employs are well within the common practise of bebop. Taken as a whole they constitute the specified surface structure that, according to the nature of the sign function, signifies a deeper content level, which we will explore further. 4.3.3. The Metric/Harmonic Frame: Harmonic Properties In our discussion of the different blues harmonisations earlier in this text, we were introduced to the idea of a virtual map outlining a measured route through a virtual space (see example 3). What I am claiming at this point is that such a map is tied to the expression level or the signified of the semiotic process of improvisation. The sign is the harmonic structure of the piece on a generic level; the signifier is a harmonic variation of this structure as expressed online; and the content level or signified is the mental representation or cognitive map of a route through a virtual physical space. Such a map will have a number of properties, which we shall explore in more detail below. My claim as to its existence is tied to the fundamental idea that musical meaning is embodied, which I derive from cognitive semantics. The cognitive map guides or frames the improvisation according to a number of metric and harmonic properties, which is why I call it the Metric/Harmonic frame (M/H frame). Let us start with the harmonic properties of the map, and let us look once more at example 3. Here the harmonic properties of the standard blues chorus were symbolised as blocks of two or four bars length, while the Coltrane-blues moved along a different path, pointing to the tonic in bar 1, the subdominant in bar 5, and the dominant in bar 9. This contrast exemplifies a marked stylistic difference between a rock-blues and a bebop-blues.[8] While rock musicians don’t give much thought to the possibilities of the dominant chord, bebop musicians excel in exploring ways to move from one chord to another: this is what the IIm7-V7 progression is all about.
Example 8
 Example 8 shows us the M/H frame for the first 16 bars of “Ornithology”. The salient points, harmonically, are the G in bar 1, the F in bar 5, the Eb in bar 9, the Gm in bar 11 and the G in bar 17 (not shown here). These are some of the necessary indicators of the form, identifying this piece as Ornithology/How High the Moon and none other. Following each of these points there is a period, marked as a dashed line, where we harmonically stay in the same area. The stable period is flexible, but typically takes up half of the time between one point and the next, the other half showing a prolonged arrow that indicates a movement towards the next point (the exception being the long “turnaround” before moving into the second half of the chorus). Such a movement I referred to above as one of the characteristic strategies of bebop, where musicians negotiate the change from one chord to the next through various means, mainly centred on setting up directional tension or dissonance, which will lead tonality in a specific direction (the IIm7-V7 progression and everything that can be derived from it). In jazz there has been a huge effort towards creating a large variety of ways to prepare or “set up” a chord shift, not only through chord substitutions, but also through the use of alternate scales (e.g. altered and diminished scales) and melodic devices. For clarity ex. 9 shows the full semiotic structure of the first 16 bars of Ornithology.
Example 9
 Before leaving the harmonic properties of the M/H frame we shall take a note for later use. Playing through the changes of Ornithology we experience a constant shifting back and forth between on the one side a stable harmonic level – the G, the F etc. – and on the other side a movement towards the next stable tonal level (the arrow), or in other words between a harmonic state and a harmonic event. This observation will be useful when we are going to discuss the narrative aspect of the chorus. But before doing so, let us look at the metric properties of the M/H frame. 4.3.4. The Metric/Harmonic Frame: Metrical Properties The metrical properties are at least as important for guiding the improvisation as the harmonic properties, but because of their apparent simplicity they are often overlooked in a discussion of jazz improvisation. They constitute the ground not only for a chord-based approach to improvisation, but also for a melody-based approach such as we meet in so- called swing music, which is one reason why swing and bebop musicians could mutually benefit from playing, for instance, How High the Moon/Ornithology together. You could say that the metrical properties measure out the distances; they quantify the route, while the harmonic properties qualify it. Or, to put it differently, the metric properties determine when to proceed, while the harmonic properties tell you how to proceed. The thirty-two bars of “Ornithology” subdivide into two 16-bar segments, and these subdivide once more into four 8-bar segments. The first and the third of these are similar, which is why we call it an ABAC-form. Let us look at example 5 again to see the HT of the whole chorus and compare with example 9. The first A is nicely symmetrical, as it subdivides into two similarly shaped 4-bar segments one whole step apart, and these again subdivide into roughly two bars of state and two bars of event. Counting 2-bar units we get a simple progression of STRONG-weak-Strong-weak(for a discussion of the impact of the strong-weak paradigm on harmonic architecture see Nettles & Graf, 1997). This repeats itself in the second A, with the one exception that this time you know it is the second time around, you know that you did this once before and that this time you are going on in a different direction than the first time (although amateur musicians often negotiate their way from chord to chord, expert musicians know exactly where they are at any given moment). The second half of the two 16-bar segments, the B and the C, are not symmetrical. They do not subdivide into two 4-bar segments as naturally as the A-sections do. They could both subdivide into four bars + four bars as well as into two bars + six bars, where the first 2-bar segment (which is identical for B and C) is like a diminished version of the 4-bar segments in A: the state/event shift compressed into half the space. What’s more, at this place we meet with a significant point of formal contrast between the B and the C: the Gm in bar 11 vs. the G in bar 27. We are returning to the tonic chord (in the C-section) or to its minor “sister” (in the B-section) at a point, which holds an unstable position in the 4 bar metrical grid that was established in the A-section. The point of return to the tonic, the third of the 4 bars, is felt to be less strong than the first of these 4 bars, where we hit the point of greatest contrast to the tonic, the Eb. Not only has the metrical balance been upset, but the subdivision is ambiguous, as the bars 11-12 in the B-section and 27-28 in the C-section harmonically could belong to the group before them as well as to the group coming after them. The rest of the two 8-bar segments (B and C respectively) is spent in regaining the metrical equilibrium, and in establishing the tonic chord in a more convincing way. Hence the long turnaround in B, which leads straight into two bars of G in the next A-section. And hence the two 2-bar turnarounds at the end of C. Notice here the doubling of the harmonic rhythm. Furthermore, notice especially the perhaps most prominent contrast between the B and the C: the G in bar 31. Where the B-section uses 4 bars to prepare the jump into G at the beginning of the second A, the C-section “hits home” 2 bars before the end, allowing the soloist and everybody else a breathing space to ease out of the chorus and prepare for the next. This rather meticulous pointing out of occurrences in the HT that may seem obvious serve the purpose of stressing the importance of the metric properties, which are often overlooked. The point is not that a G chord occurs in bar 31, which would be important if you make your way from chord to chord, but that you have it firmly fixed in your mind, as part of the route description, that you are going to play a ‘turnaround’ in the last two bar segment. 4.4. Narrativity in Jazz This study is based on the idea that humans are semiotic beings who employ a number of strategies in order to make sense of the world. Among these is the sign function, which is understood as an intrinsic cognitive mechanism evoking cognitive responses to perceived elements such as musical phrases. The inverse strategy in which musical phrases are used expressively to generate meaning can be studied in jazz improvisation as we have seen. We have explored the HT as a sign function and the improvisational act as a semiotic process through which meaning is unfolded within a biplanar semiotic setting with an expression level and a content level.[9] And we have argued that the content level of the sign can be understood as, or may even be experienced as, a journey through physical space, or at least a mental representation of such a journey. This means we are speaking of a cognitive map that represents a route through virtual space, which - in the case of bebop - takes the form of an M/H-frame, guiding and constraining the expressive act. We could compare this phenomenon with a children’s game that has a set of rules concerning times, places and ways to perform, along with a considerable amount of freedom to play. What I want to do now is to explore the diachronic aspects of the content structure of the sign: the journey-as-story. 4.4.1. The Narrative In example 10 I have positioned the salient points of the M/H frame of “Ornithology” in a grid like the one used for the basic blues structure in example 3. As you can see the manner of representation is similar to the way the Coltrane-blues was represented, reflecting the improvisational strategy of the bebop musician. It is easy to interpret this as a map of a route through space. But how will this be understood as a story?
Example 10
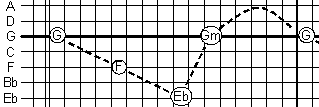 The straightforward answer to this question is found in cognitive science, where it is held that even the simplest constellations are interpreted by the mind as stories (Johnson, 1987; Lakoff, 1987; Turner, 1996; Lakoff & Johnson, 1999, and Imberty, 2001). Simple stories, we can call them proto-narratives, are clusters of events leading from one state to another. Understanding such stories metaphorically as a movement from one position in space to another involves what Lakoff calls the SOURCE-PATH-GOAL schema (Lakoff 1987). In such a schematized story a harmonic structure that begins in the tonic key, proceeds to another key, and finally returns to the tonic. This will be a story of a journey through space – one of the enjoyable ones that can be told again and again (hence the room for variations!). Cognitive scientists, semioticians and others believe that human beings always create stories, and that we have an innate drive to understand everything that happens to us and in the world by incorporating it into a narrative framework. In fact this is what understanding means: to insert single events into familiar contexts. That was the simple answer. The more complex answer involves a semiotic perspective, and I shall base my suggestion on the narrative theory of the French semiotician A.-J. Greimas (Greimas 1979; for an introduction to narrative theory see Monelle 1992). He claimed that a narration has a surface syntax, a deep syntax, and a narrative core. The narrative surface syntax is the unfolding of the story as we meet it; the deep syntax is a temporal schema, based on the central issue or narrative core, which constrains the telling of the story; and the narrative core, the “topic” of the story, consists of the dynamic relations between two oppositional terms: black > < white; night > < day; good > < evil. The conventional way stories are told in films is a good example of this. A film has a beginning, a middle and an end. The beginning moves from a state of equilibrium to the introduction of a conflict (an opposition), which is often personified (black hat-white hat). The middle develops a number of dynamic constellations of this conflict along with a way to resolve it. And the end creates the solution and brings us to a new state of equilibrium. Such a structure represents the unfolding of the narrative core into a deep narrative syntax, which again is transformed to surface syntax in the actual telling of the story. According to Greimas and his associates this whole dynamic complex of narrative surface, deep syntax and core is present in all forms of human expression (Greimas & Courtés, 1979).
Example 11
Ornithology operates harmonically in an opposition between the tonal levels of G and Eb. If we insert the pivotal information of the narrative path of Ornithology into the semiotic square, we can represent the basic syntactic structure of the M/H-frame like this:
Example 12
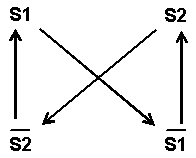 The core opposition between G and Eb unfolds in a cycled patterned movement. Something (a IIm7-V7) forces the subject to abandon his home-position, G, and move to F (not-G). Continued movement will logically lead to Eb (the oppositional term). In order to recapture the original state of equilibrium, the subject must bring itself to the dominant position, which means reaching the D7. From here the tension is released naturally, the subject is brought back to its original state and the cycle is completed.[10] One might argue that the simple structure of a 16 bar form does not capture all the richness and the analytical perspectives of a Wagnerian narrative in a way comparable to Tarasti’s treatment in Myth and Music (Tarasti 1979). This is why I have introduced the term proto-narrative above, alluding to a body of research on infant musicality and semiosis (see especially Trevarthen 1994). My argument is twofold. First, our most sophisticated skills are developed from and rest upon extremely simple ones; and, second, the reason why highly developed cultural artefacts move us so deeply might well be that they reach out to deep, mythical levels in our being, levels that originate in our mythical, preverbal layers of consciousness.[11] I am not claiming that a children’s song or the structure of How High the Moon is directly comparable with Götterdämmerung, merely that vital features of the narrative structure are the same. Before leaving the topic of narrative theory and its application to music, it is worthwhile bringing another aspect to attention. We have dealt with the narrative core and the deep syntax, but it appears that even on the surface level a harmonic construction like Ornithology unfolds according to the principles of narrative theory. According to Greimas, the narrative surface syntax consists of a syntagmatic chain of what he calls narrative programs. A narrative program (NP) is the basic unit of the articulated story, which unfolds in time through the linking together of NPs. An NP consists of two elements: an enunciation of doing, which on its side controls an enunciation of state, or in other words an event-related utterance and a state-related utterance. During the discussion of examples 8 and 9, we made a note of how the harmonic structure could be broken down to a succession of states, which were the harmonically stable parts, and events, the harmonically dynamic parts or dominant constructions which were in a manner of speaking in control of the succeeding states. Consequently we can read the M/H-frame as a succession of events (arrows) and states (circled chord roots). 4.5. Conclusion We have set out to approach jazz improvisation as a semiotic process, to explore the unfolding of the sign structure, and to investigate the content structure of the sign as a narrative pathway. During this procedure we have mainly concentrated on the chord changes, the material for traditional music analysis. There are, of course, other parameters involved in the musical semiosis than the harmonic one. A more complete picture should not only include rhythm and melody, intensity, curve and timbre, but also factors as the sociocultural framing, which influences the personal expressiveness of the artist (the situatedness). Nonetheless, I hope that the material presented here has shown that a semiotic approach can provide a very rich approach. It can not only tell us something essential about the piece being investigated, but together with cognitive science it offers a range of tools that can help us to compare and bring to the foreground a number of distinctive stylistic features. It has long been held that musicology has too little to offer the analysis of jazz and popular music, and that the gap between analysis and the actual experience of the music is too great to make any real sense. Semiotics can help bridge that gap, and may lead us further towards musical meaning as a many-layered thing, which involves and expresses human experience in a very complete way.
To refer to this article: click in the target section |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||